How to find the focal point of a parabolohedron
The build steps shown here correspond to successive views chosen from the pick list in the 3D view above.
The parabolahedron’s construction starts with a unit length strut on the positive X, Y and Z axes.
An affine hexagon is constructed on each of the XY, YZ and ZX planes using pairs of the initial struts as edges.
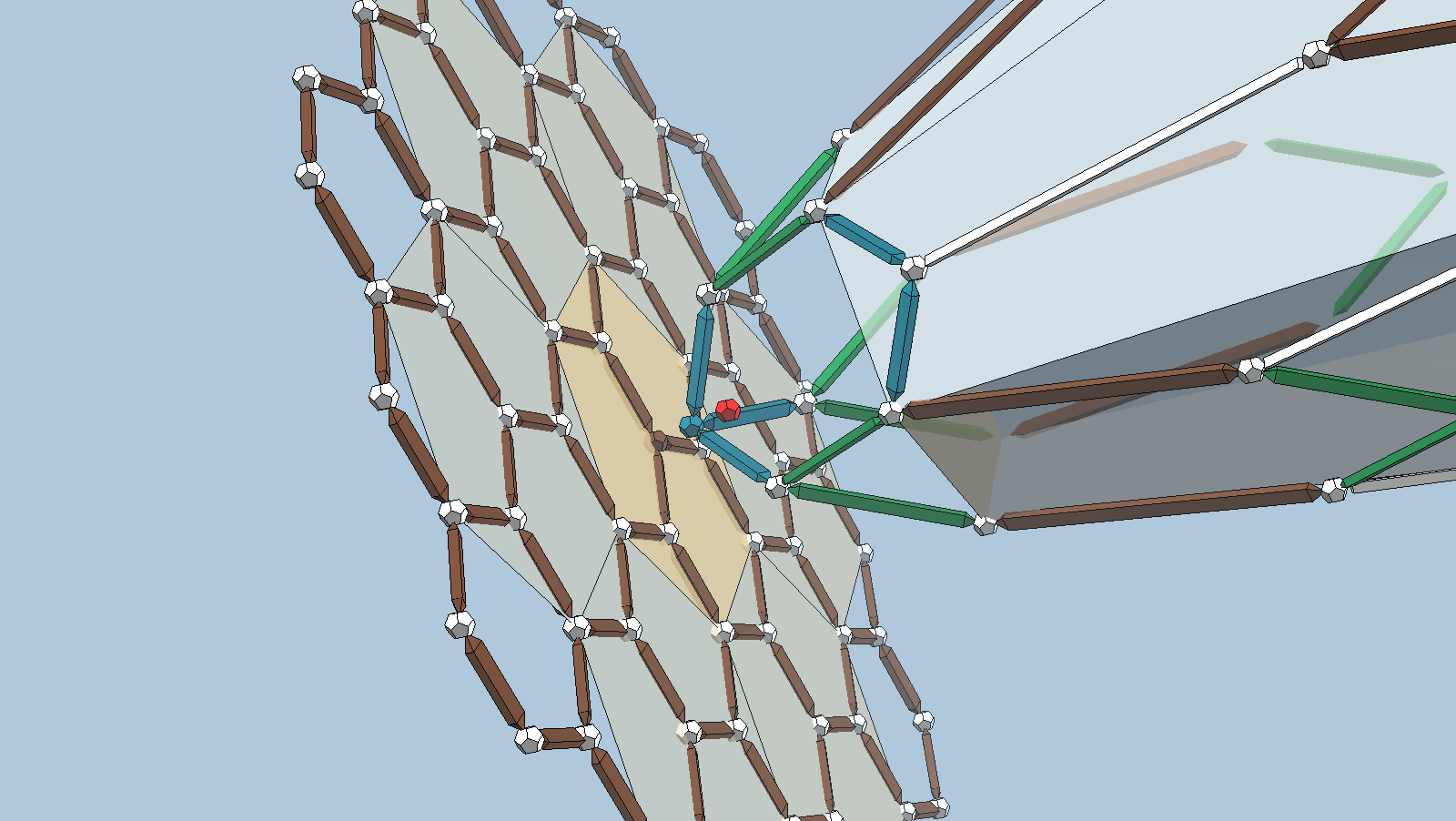
The six vertices at the end of the green struts farthest from the origin form a regular hexagon. A green strut from any one of them to their midpoint is the radius of the circular paraboloid at that point. A yellow strut from the same midpoint to the origin is the depth of the paraboliod at that point.
Using the blue strut as a unit length, the radius (green strut) is √2 and the depth (yellow strut) is √3. The focal point is calculated from these two lengths as shown in this PDF document. In this case, the distance from the origin to the focal point is √3/6 which is indicated here by the red ball. It turns out that it’s also half way between the origin and the midpoint of the initial three vertices.
Three hexagons don’t make a visually convincing paraboloid, so let’s extend it a few times. This will also be useful in showing the relationship between the vertex-first and face-first projections. Oops, ignore that extra yellow strut near the opening of the paraboloid.
The directrix plane is the same distance from the origin as the focal point, but in the opposite direction. Here the affine hexagonal facets are projected onto the directrix plane where they become regular hexagons.
The distance from the focal point to any point on the paraboloid is equal to the perpendicular distance from that same point to the directrix plane. Viewing this file in vZome desktop allows any such pair to be selected and the measure tab will show that they are exactly equal in length.
A face-first projection can be generated from a subset of the vertices generated by the vertex-first process. It’s noteworthy that this results in the focal point being outside of the resulting parabolahedron in contrast to the vertex-first version. Also, the individual facets of the face-first projection are 3 times greater in area than the vertex-first projection of the same parabolahedron. This means a vertex-first projection provides 3 times more accurate approximation of a paraboloid than the face-first representation and thus, would probably perform better as a parabolic reflector.