A polyhedron made by folding eight regular pentagons
One of the 8 ways to join regular pentagons per Matt Parker’s video
and described in this PDF.
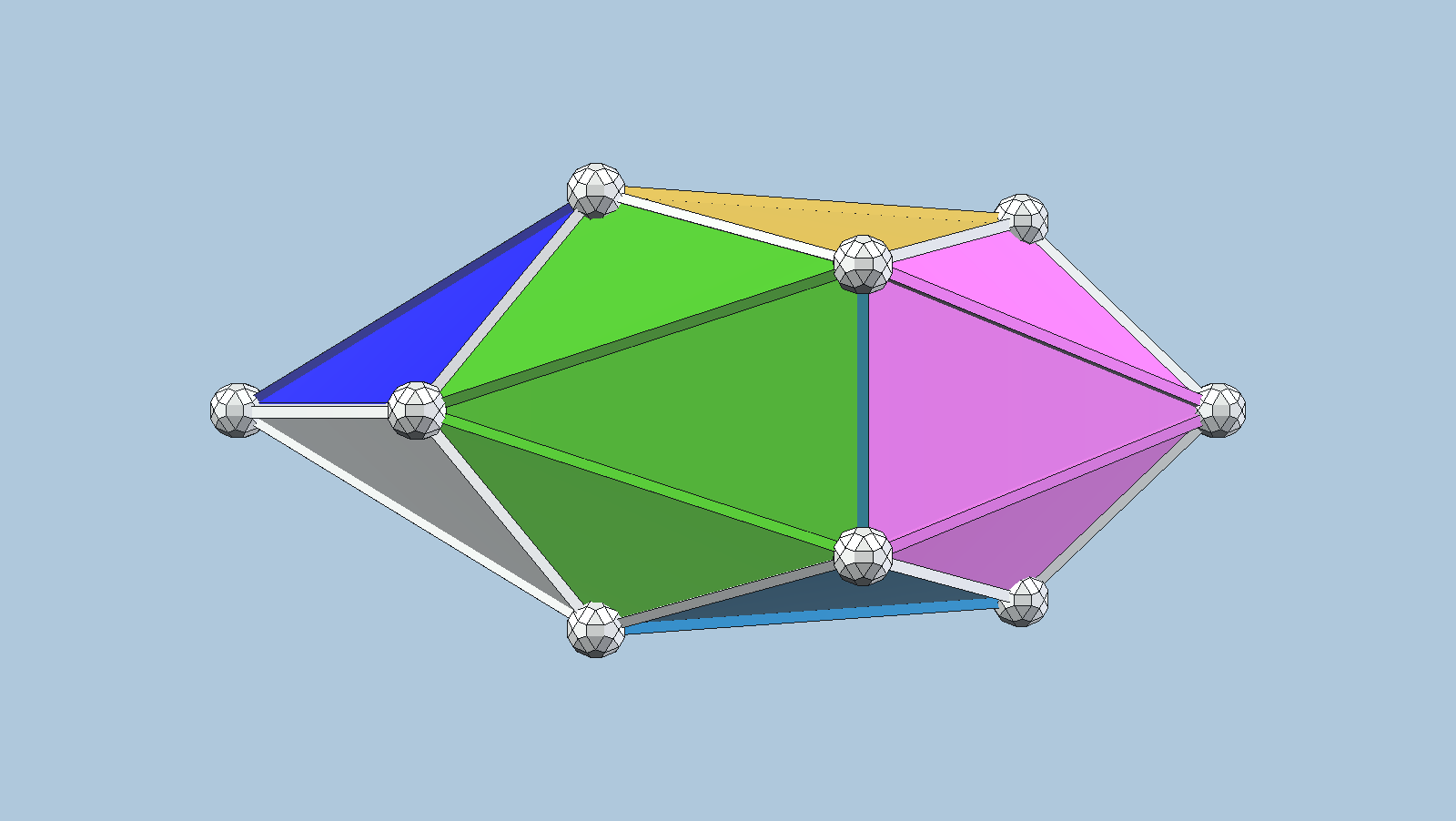
This model cannot be built exactly using any of the algebraic fields supported by vZome. This model is a rational approximation accurate to 5 decimal places. The exact values used in the coordinates are determined by this set of simultaneous equations:
\(d^2 + c^2 + b^2 -2bc - 1 = 0\)
\(f^2 + d^2 + b^2 + a^2 - 2ab - d - \frac{ 3 } { 4 } = 0\)
\(f^2 + 2a^2 - f - \frac{ 1 } { 4 } = 0\)
\(f^2 + c^2 +a^2 - 2ac - \phi - \frac{ 3 } { 4 } = 0\)
\(f^2 + d^2 +b^2 + a^2 - 2df + 2ab - \phi - \frac{ 3 } { 4} = 0\)
Where \(\phi = \frac {1 + \sqrt{5}} {2}\) is the golden ratio.