Solving the fold-and-cut problem for the Spectre tile
David Richeson nerd sniped me!!! This design is part of my response.
The puzzle he proposed was to fold a sheet of paper so that a single straight cut will produce a spectre tile.
David published his solution along with a comparable solution for the hat tile. He refered to the work of Erik Demaine et al, which provides two algorithms for solving the general case.
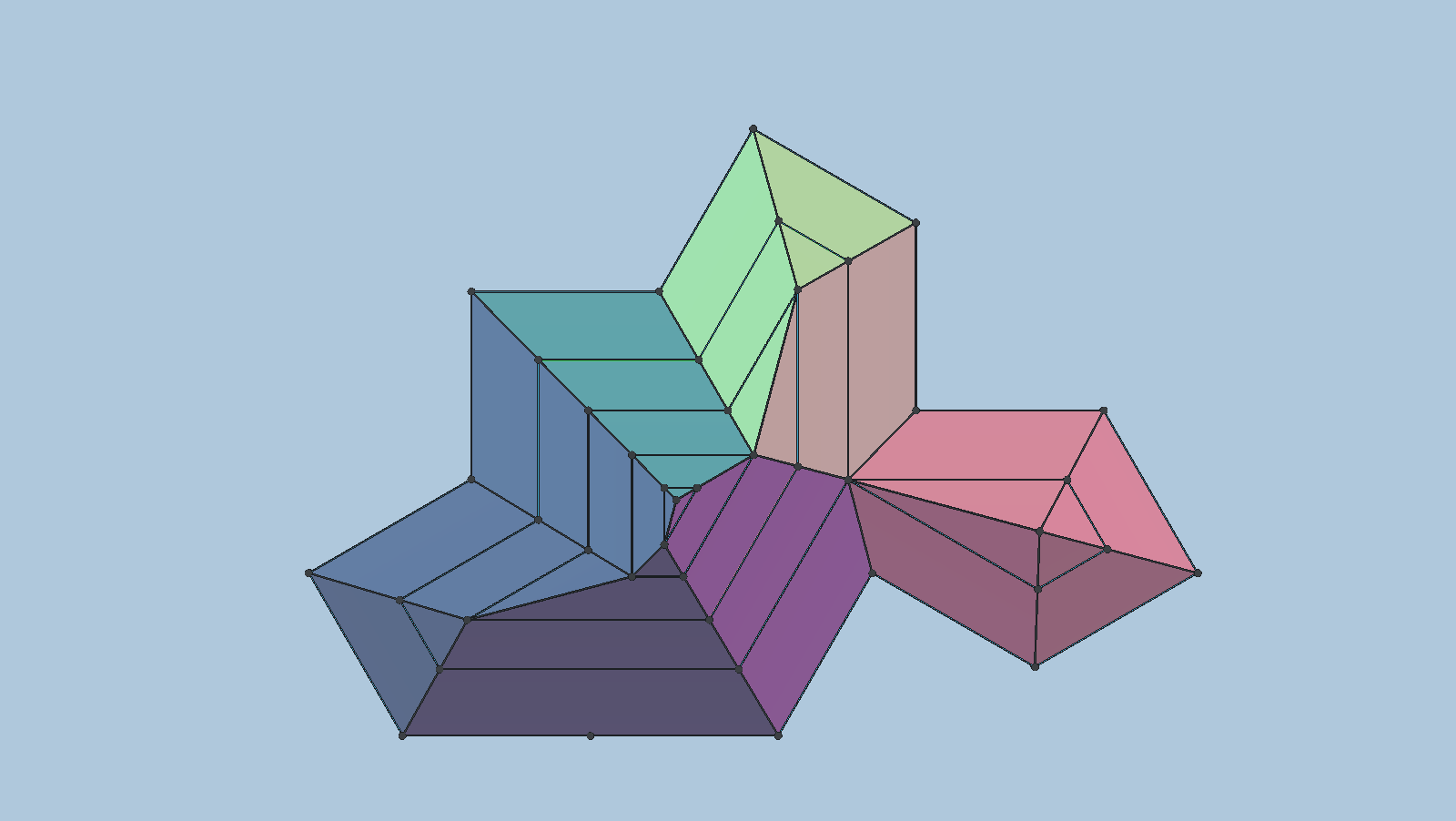
Dermaine calls one approach the Disk Packing Method. The other algorithm, which is more suited for vZome, he calls the Straight Skeleton Method. It is based in part on this 1995 paper published in the Journal of Universal Computer Science.
That paper describes the algorithm and how it is analagous to building a constant-pitch roof on an arbitrary set of straight walls (the polygon). The specific pitch is irrelevant, but must be constant for all facets of the roof. The end result is that the resulting ridge line can be projected onto the polygon’s plane (the spectre in our case) and the projection of the various vertices of the ridge line serve as a starting point for producing the necessary folds.
This design includes several views of that approach. It can be seen that the resulting ridge line projections corespond exactly to folds in David’s solution.